Entier (Integer)

Un entier est un nombre sans partie décimale ou avec une partie décimale nulle (pas une fraction), qui peut être positif, négatif ou égal à zéro.

Par exemple : -5, 1, 5, 8, 97 et 3 043.

Les nombres suivants ne sont pas des nombres entiers : -1,43, 1 3/4, 3,14, 0,09 et 5 643,1.

L'ensemble des entiers relatifs, noté Z, est formellement défini comme suit :

Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}

Dans les équations mathématiques, les entiers inconnus ou non spécifiés sont représentés par des lettres du milieu de l'alphabet, notées en minuscules et en italiques. Les plus courantes sont p, q, r et s.

L'ensemble Z est dit dénombrable. Un ensemble est dit dénombrable lorsque ses éléments, bien qu'en nombre infini, peuvent être listés sans omission ni répétition dans une suite indexée par les entiers. Par exemple, à partir de la liste {..., -3, -2, -1, 0, 1, 2, 3, ...}, on peut déduire que 356 804 251 et -67 332 sont des entiers, tandis que 356 804 251,5, -67 332,89, -4/3 et 0,232323 n'en sont pas.

Les éléments de Z peuvent être associés un à un avec les éléments de l'ensemble des entiers naturels, noté N, sans qu'aucun élément ne soit exclu d'un ensemble ni de l'autre. Soit N = {1, 2, 3, ...}. L'association peut être comme suit :

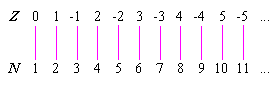
Dans les ensembles infinis, l'existence d'une correspondance une à une est le test décisif permettant de déterminer la cardinalité (la taille) de l'ensemble. L'ensemble des nombres naturels et celui des nombres rationnels ont la même cardinalité que l'ensemble Z. Mais l'ensemble des nombres réels, celui des nombres imaginaires et celui des nombres complexes ont une cardinalité supérieure à celle de Z.