Régression linéaire ?
La régression linéaire est une technique statistique qui identifie la relation entre la valeur moyenne d'une variable et les valeurs correspondantes d'une ou plusieurs autres variables. En comprenant la relation entre les variables, la technique de régression linéaire peut aider les scientifiques des données (data scientists) à modéliser et à prédire comment une variable va évoluer par rapport à une autre. Cela peut impliquer des analyses telles que l'estimation des ventes en fonction des prix des produits ou la prévision du rendement des cultures en fonction des précipitations. À un niveau élémentaire, le terme « régression » signifie revenir à un état antérieur ou moins développé.
La régression linéaire dans l'apprentissage automatique (ML) s'appuie sur ce concept fondamental pour modéliser la relation entre les variables à l'aide de diverses techniques d'apprentissage automatique afin de générer une ligne de régression entre des variables telles que le taux de vente et les dépenses marketing. Dans la pratique, l'apprentissage automatique tend à être plus utile lorsqu'il s'agit de travailler avec plusieurs variables, ce qu'on appelle la régression multivariée, où les relations entre elles nécessitent des coefficients de régression plus complexes.
La régression linéaire est un élément fondamental de l'apprentissage supervisé. Elle permet essentiellement de déterminer si une variable explicative peut aider à prédire le résultat d'une autre variable. Par exemple, les dépenses publicitaires consacrées à un média plutôt qu'à un autre ont-elles un impact significatif sur les ventes ?
Dans le cas le plus simple, la régression linéaire tente de prédire la valeur d'une variable, appelée variable dépendante, à partir d'une autre variable, appelée variable indépendante. Par exemple, si une organisation essayait de prédire le taux de vente en fonction des dépenses publicitaires, les ventes seraient la variable dépendante, tandis que les dépenses publicitaires seraient la variable indépendante.
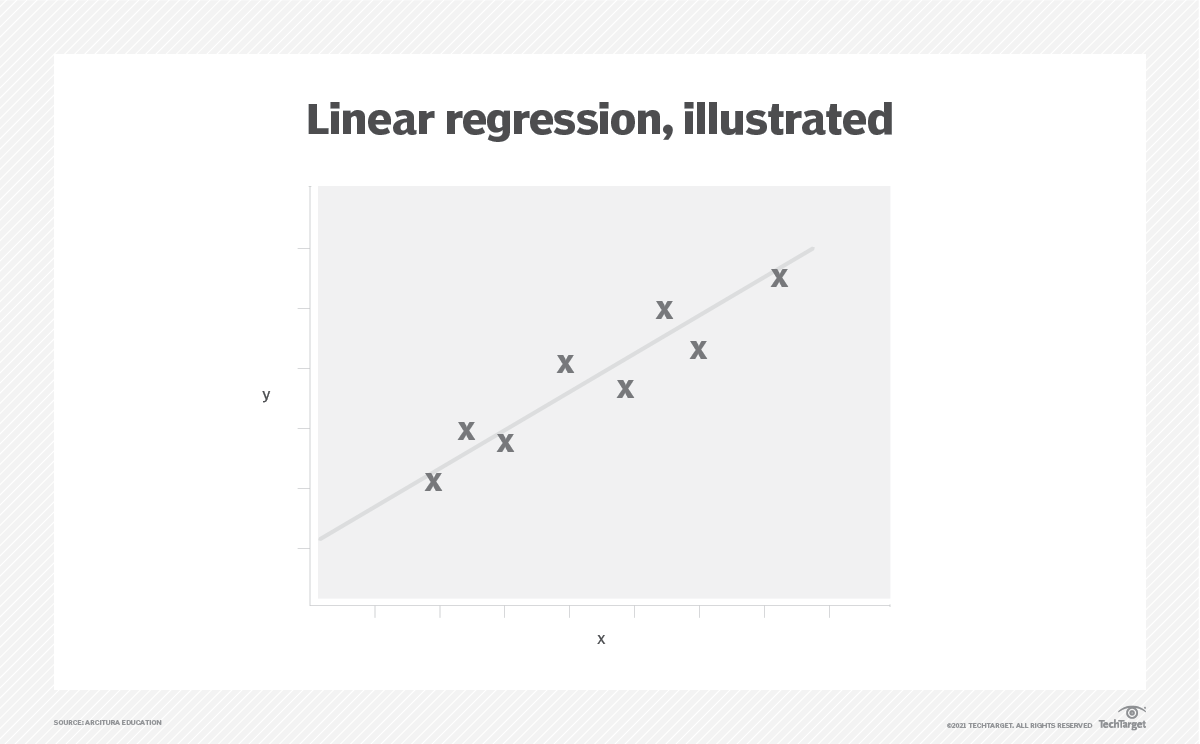
La régression linéaire est linéaire dans la mesure où elle guide le développement d'une fonction ou d'un modèle qui s'adapte à une ligne droite (appelée ligne de régression linéaire) sur un graphique représentant les données. Cette ligne minimise également la différence entre une valeur prédite pour la variable dépendante et la variable indépendante correspondante.
Dans le cas de l'estimation du taux de vente, chaque dollar de vente peut augmenter régulièrement dans une certaine fourchette pour chaque dollar dépensé en publicité, puis ralentir une fois que le marché publicitaire atteint un point de saturation. Dans ces cas, des fonctions plus complexes doivent être construites à l'aide de statistiques ou de techniques d'apprentissage automatique afin d'ajuster les données sur une ligne droite.
Pourquoi la régression linéaire est-elle importante ?
La régression linéaire est importante pour les raisons suivantes :
- Il fonctionne avec des données non étiquetées.
- C'est relativement simple et rapide.
- Il peut être appliqué comme élément fondamental dans les domaines des affaires et des sciences.
- Il prend en charge l'analyse prédictive.
- Il s'applique facilement aux modèles ML.
Types de régression linéaire
Il existe trois principaux types de régression linéaire :
- Régression linéaire simple. La régression linéaire simple trouve une fonction qui relie les points de données à une ligne droite sur un graphique à deux variables.
- Régression linéaire multiple. La régression linéaire multiple trouve une fonction qui relie les points de données à une ligne droite entre une variable dépendante, comme les ventes de crème glacée, et une fonction de deux variables indépendantes ou plus, telles que la température et les dépenses publicitaires.
- Régression non linéaire. La régression non linéaire trouve une fonction qui ajuste deux variables ou plus sur une courbe plutôt que sur une ligne droite.
Au-delà de ces trois catégories fondamentales, il existe toutefois de nombreuses méthodes spécifiques de régression linéaire, parmi lesquelles on peut citer les suivantes :
- Modélisation linéaire hiérarchique (HLM).
- Régression par lasso.
- Régression logistique.
- Régression ordinale.
- Moindres carrés ordinaires.
- Régression par moindres carrés partiels.
- Régression polynomiale.
- Régression en composantes principales.
- Régression quantile.
- Régression de crête.
- Modélisation par équations structurelles.
- Régression de Tobit.
Chaque approche spécifique peut être appliquée à différentes tâches ou à différents objectifs d'analyse des données. Par exemple, le HLM (également appelé modélisation multiniveaux) est un type de modèle linéaire destiné à traiter des structures de données imbriquées ou hiérarchiques, tandis que la régression ridge peut être utilisée lorsqu'il existe une forte corrélation entre les variables indépendantes, ce qui pourrait autrement entraîner un biais involontaire avec d'autres méthodes.
Exemples de régression linéaire
Les points suivants mettent en évidence trois utilisations courantes de la régression linéaire :
- Il peut être utilisé pour identifier l'ampleur de l'effet qu'une variable indépendante, comme la température, pourrait avoir sur une variable dépendante, comme les ventes de crème glacée.
- Il peut être utilisé pour prévoir l'impact des changements induits par la variable indépendante, par exemple, l'augmentation des ventes de crème glacée en fonction des différents niveaux de publicité.
- Il peut être utilisé pour prédire les tendances et les valeurs futures, par exemple la quantité de crème glacée à stocker pour répondre à la demande si la température devrait atteindre 32 °C.
Cas d'utilisation de la régression linéaire
Les cas d'utilisation typiques de la régression linéaire dans le domaine des affaires sont les suivants :
- Élasticité des prix. De combien les ventes baisseront-elles si le prix augmente d'un montant donné ?
- Gestion des risques. Quelle est la responsabilité prévue pour une tempête d'une intensité donnée ?
- Contrats à terme sur matières premières. Quel est le lien entre les précipitations et le rendement des cultures ?
- Détection des fraudes. Quelle est la probabilité qu'une transaction soit frauduleuse ?
- Analyse commerciale. Dans quelle mesure les ventes pourraient-elles augmenter avec différents niveaux d'incitations au partage des bénéfices ?
Avantages et inconvénients de la régression linéaire
Les avantages de la régression linéaire sont les suivants :
- Il facilite l'analyse exploratoire des données.
- Il permet d'identifier les relations entre les variables.
- C'est relativement simple à mettre en œuvre.
Les inconvénients de la régression linéaire sont les suivants :
- Cela ne fonctionne pas bien si les données ne sont pas vraiment indépendantes.
- La régression linéaire ML est sujette à un sous-ajustement qui ne tient pas compte des événements rares.
- Les valeurs aberrantes peuvent fausser la précision des modèles de régression linéaire.
Hypothèses clés de la régression linéaire
La régression linéaire nécessite que l'ensemble de données prenne en charge les propriétés suivantes :
- Les données doivent être organisées sous forme de séries continues, telles que le temps, les ventes en dollars ou les dépenses publicitaires. Cela ne fonctionne pas directement avec des données qui se présentent sous forme de catégories telles que les jours de la semaine ou les types de produits. Les mesures doivent être effectuées de manière cohérente.
- La variable réponse forme une relation linéaire entre les paramètres et les variables prédictives. Étant donné que les variables prédictives sont considérées comme des valeurs fixes, la linéarité consiste simplement à définir correctement les paramètres.
- Les observations doivent être véritablement indépendantes les unes des autres. Par exemple, les ventes et les bénéfices peuvent ne pas être indépendants si le coût des marchandises ou d'autres facteurs n'affectent pas les bénéfices séparément.
- Les données doivent être nettoyées de toute valeur aberrante ou événement rare, c'est-à-dire des problèmes liés à la qualité des données.
- La variation de chaque point de données par rapport à la ligne droite doit être constante pour tous les changements de la variable indépendante. Cette variance constante est appelée homoscédasticité.
- Bien que les observations ou les points de données soient des valeurs aléatoires, les variables prédictives peuvent être traitées comme des valeurs fixes. C'est ce qu'on appelle l'exogénéité faible.
Outils de régression linéaire
Les méthodes de régression linéaire peuvent être réalisées sur papier, mais le processus peut s'avérer fastidieux et impliquer des sommes et des carrés répétitifs. Dans l'enseignement supérieur et les applications professionnelles des équations de régression linéaire, on utilise généralement des logiciels pour ingérer les données et effectuer rapidement les processus mathématiques requis. La régression linéaire est prise en charge par de nombreux outils logiciels et bibliothèques de programmation, notamment les suivants :
- Logiciels statistiques spécialisés tels que IBM SPSS Statistics.
- Travail
- Microsoft Excel.
- Régression linéaire R.
- Scikit-learn.
Régression linéaire vs régression logistique
La régression linéaire n'est qu'une catégorie parmi d'autres techniques de régression permettant d'ajuster des nombres sur un graphique.
La régression multivariée peut ajuster les données à une courbe ou à un plan dans un graphique multidimensionnel représentant les effets de plusieurs variables.
Bien que la régression logistique et la régression linéaire utilisent toutes deux des équations linéaires pour établir des prévisions, la régression logistique prédit si un point de données donné appartient à une classe ou à une autre, par exemple spam/non spam pour un filtre de courrier électronique ou fraude/non fraude pour un organisme d'autorisation de cartes de crédit.
Découvrez ce que sont l'apprentissage supervisé, non supervisé et semi-supervisé, et comment les algorithmes d'apprentissage automatique sont utilisés dans diverses applications commerciales.









