Qu'est-ce que la régression logistique ?

Comment fonctionne la régression logistique dans l'apprentissage automatique et la modélisation prédictive ?

La régression logistique dans l'apprentissage automatique a pris beaucoup d'importance en tant qu'algorithme d'apprentissage supervisé. Elle permet aux algorithmes utilisés dans les applications d'apprentissage automatique de classer les données entrantes en fonction des données historiques. À mesure que des données pertinentes supplémentaires sont ajoutées, les algorithmes améliorent leur capacité à prédire les classifications au sein des ensembles de données.

En apprentissage automatique, la régression logistique est classée parmi les modèles discriminatifs, car elle vise à distinguer des classes ou des catégories. Contrairement aux algorithmes de modèles génératifs, notamment le modèle naïf de Bayes, elle ne génère pas de données ou de visuels pour représenter les probabilités ou les classes prédites, comme l'image d'un chat.

La régression logistique peut également jouer un rôle dans les activités de préparation des données en permettant de classer les ensembles de données dans des compartiments prédéfinis spécifiques pendant le processus d'extraction, de transformation et de chargement afin de préparer les informations en vue de leur analyse.

La régression est l'un des piliers des applications modernes d'analyse prédictive.

« Les outils d'analyse prédictive peuvent être classés de manière générale en deux catégories : les outils traditionnels basés sur la régression et les outils basés sur l'apprentissage automatique », explique Donncha Carroll, associé au sein du département Croissance des revenus de Lotis Blue Consulting.

Les modèles de régression représentent ou encapsulent une équation mathématique qui approxime les interactions entre les variables modélisées. Les modèles d'apprentissage automatique utilisent et s'entraînent sur une combinaison de données d'entrée et de sortie, et utilisent également de nouvelles données pour prédire la sortie.

Quel est l'objectif de la régression logistique ?

La régression logistique remplit plusieurs fonctions clés dans l'analyse statistique, la classification et l'analyse prédictive :

• Classification et analyse prédictive. La régression logistique simplifie les calculs mathématiques permettant de mesurer l'effet de plusieurs variables (par exemple, l'âge, le sexe, l'emplacement publicitaire) sur un résultat donné (par exemple, le taux de clics, l'ignorance). Les modèles obtenus permettent de distinguer avec précision l'efficacité relative de différentes interventions pour différentes catégories de personnes, telles que les jeunes/les personnes âgées ou les hommes/les femmes.
• Prédiction de résultats binaires. La régression logistique est idéale pour analyser des scénarios avec une variable dépendante binaire, prédisant des résultats possibles tels que oui ou non sur la base de données antérieures. Son efficacité à cet égard en fait un outil incontournable dans des domaines tels que le marketing, la finance et la science des données.
• Apprentissage automatique. Les modèles logistiques peuvent également transformer des flux de données brutes afin de créer des fonctionnalités pour d'autres types d'IA et de techniques d'apprentissage automatique. En fait, la régression logistique est l'un des algorithmes couramment utilisés dans l'apprentissage automatique pour les problèmes de classification binaire, qui sont des problèmes comportant deux valeurs de classe, y compris des prédictions telles que ceci ou cela, oui ou non, et A ou B.
• Estimation de probabilité. La régression logistique permet également d'estimer les probabilités d'événements, notamment en déterminant la relation entre les caractéristiques et les probabilités de résultats. En d'autres termes, elle peut être utilisée à des fins de classification en créant un modèle qui établit une corrélation entre le nombre d'heures d'étude et la probabilité de réussite ou d'échec de l'étudiant. À l'inverse, le même modèle pourrait être utilisé pour prédire si un étudiant particulier va réussir ou échouer lorsque le nombre d'heures d'étude est fourni comme caractéristique et que la variable de réponse a deux valeurs : réussite et échec.

Quels sont les types de régression logistique ?

Il existe trois types de régression logistique :

• Régression logistique binaire. Dans la régression logistique binaire ou binomiale, la variable réponse ne peut appartenir qu'à deux catégories, telles que oui ou non, 0 ou 1, ou vrai ou faux. Par exemple, prédire si un client achètera un produit n'a que deux résultats possibles : oui ou non. La régression logistique binaire est l'un des classificateurs les plus utilisés pour la classification binaire et la méthode la plus fréquemment utilisée dans la régression logistique.
• Régression logistique multinomiale. Ce type de régression logistique est utilisé lorsque la variable réponse peut appartenir à l'une des trois catégories ou plus et qu'il n'y a pas d'ordre naturel entre les catégories. Un exemple consiste à prédire le genre d'un film qu'un spectateur est susceptible de regarder à partir d'un ensemble d'options.
• Régression logistique ordinale. Ce type de régression est approprié lorsque la variable réponse appartient à l'une des trois catégories ou plus et qu'il existe un ordre naturel entre elles. Par exemple, une entreprise peut utiliser la régression logistique ordinale pour prédire si les niveaux de satisfaction des clients seront faibles, moyens ou élevés.

Exemple de formule et de modèle de régression logistique

Le modèle de régression logistique utilise la fonction logistique pour prédire la probabilité qu'un événement se produise en fonction des valeurs des variables indépendantes. Par exemple, il peut prédire si une fissure supérieure à une certaine taille apparaîtra dans un échantillon fabriqué, si un étudiant réussira ou échouera à un examen, ou si un participant à un sondage répondra oui ou non à une question.

La probabilité est calculée à l'aide de la fonction logistique, également appelée fonction sigmoïde, qui garantit que le résultat est compris entre 0 et 1.

Voici un exemple de formule de fonction logistique.

P = 1 ÷ (1 + e^ − (a + bx))

Voici ce que représente chaque variable dans cette équation de régression logistique :

• P est la probabilité que la variable dépendante soit égale à 1.
• e est la base du logarithme naturel.
• a est l'ordonnée à l'origine ou le terme de biais.
• b est le coefficient de la variable indépendante.
• x est la valeur de la variable indépendante.

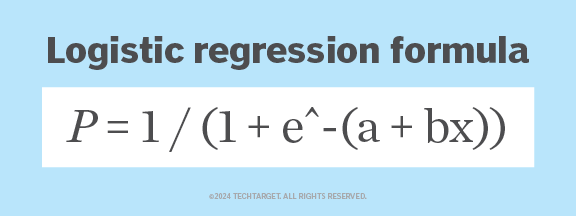
Quelles sont les hypothèses clés de la régression logistique ?

Les statisticiens et les data scientists citoyens doivent garder à l'esprit certaines hypothèses lorsqu'ils utilisent différents types de techniques de régression logistique :

1. Les variables doivent être indépendantes les unes des autres. Pour commencer, les variables doivent être indépendantes les unes des autres. Par exemple, le code postal et le sexe peuvent être utilisés dans un modèle, mais le code postal et l'État ne fonctionneraient pas. D'autres relations moins transparentes entre les variables peuvent se perdre dans le bruit lorsque la régression logistique est utilisée comme point de départ pour des applications complexes d'apprentissage automatique et de science des données. Par exemple, les scientifiques des données peuvent déployer des efforts considérables pour s'assurer que les variables associées à la discrimination, telles que le sexe et l'origine ethnique, ne sont pas incluses dans l'algorithme. Cependant, celles-ci peuvent parfois être indirectement intégrées à l'algorithme via des variables qui n'étaient pas considérées comme corrélées, telles que le code postal, l'école ou les loisirs.
2. Les données brutes doivent représenter des phénomènes non répétitifs ou indépendants. Une autre hypothèse est que les données brutes doivent représenter des phénomènes non répétitifs ou indépendants. Par exemple, une enquête de satisfaction client doit représenter les opinions de personnes distinctes. Cependant, ces résultats seraient faussés si une personne répondait plusieurs fois à l'enquête à partir de différentes adresses e-mail afin d'obtenir une récompense.
3. La relation entre les variables et le résultat doit être linéaire. Il est également important que la relation entre les variables et le résultat puisse être linéaire via des cotes logarithmiques ou des cotes logarithmiques, ce qui est un peu plus flexible qu'une relation non linéaire.
4. La régression logistique nécessite également un échantillon de taille significative. La régression logistique nécessite également un échantillon de taille significative. Celui-ci peut être aussi petit que 10 exemples de chaque variable dans un modèle. Cependant, cette exigence augmente à mesure que la probabilité de chaque résultat diminue.
5. Chaque variable peut être représentée à l'aide de catégories binaires. Une autre hypothèse de la régression logistique est que chaque variable peut être représentée à l'aide de catégories binaires telles que masculin ou féminin, clic ou pas de clic. Une astuce particulière est nécessaire pour représenter des catégories comportant plus de deux classes. Par exemple, on peut transformer une catégorie comportant trois tranches d'âge en trois variables distinctes, chacune spécifiant si un individu appartient à cette tranche d'âge.

Applications de la régression logistique dans le domaine des affaires

La régression logistique a diverses applications dans le domaine des affaires. Parmi les cas d'utilisation notables de la régression logistique, on peut citer les suivants :

• Optimisation des stratégies. Les organisations utilisent les informations issues des résultats de la régression logistique pour améliorer leur stratégie commerciale afin d'atteindre leurs objectifs commerciaux, tels que la réduction des dépenses ou des pertes et l'augmentation du retour sur investissement des campagnes marketing. Une entreprise de commerce électronique qui envoie des offres promotionnelles coûteuses à ses clients, par exemple, voudra savoir si un client particulier est susceptible de répondre à ces offres ou non (c'est-à-dire si ce consommateur sera réceptif ou non). En marketing, cela s'appelle la modélisation de la propension à répondre. De même, une société émettrice de cartes de crédit développera un modèle pour l'aider à prédire si un client va se trouver en défaut de paiement sur sa carte de crédit en se basant sur des caractéristiques telles que son revenu annuel, ses paiements mensuels par carte de crédit et le nombre de défauts de paiement. Dans le jargon bancaire, cela s'appelle la modélisation de la propension au défaut de paiement.
• Prévision du taux de désabonnement. La régression logistique aide les entreprises à prévoir le taux de désabonnement ou d'annulation d'abonnement en examinant les données historiques et divers facteurs pertinents associés au comportement des clients. Ces facteurs peuvent inclure des informations démographiques, l'historique des achats, la fréquence des interactions, les scores de satisfaction client et les indicateurs d'engagement. En analysant ces variables, les modèles de régression logistique peuvent identifier des modèles et des relations qui correspondent à la probabilité de désabonnement.
• Détection des fraudes. Dans le secteur financier, la régression logistique est utilisée pour détecter les transactions frauduleuses. En analysant les montants des transactions et les cotes de crédit, les modèles de régression logistique peuvent évaluer la probabilité qu'une transaction soit frauduleuse, contribuant ainsi à améliorer les mesures de détection des fraudes.

Cas d'utilisation de la régression logistique dans l'industrie

La régression logistique est devenue particulièrement populaire dans le domaine de la publicité en ligne, aidant les spécialistes du marketing à prédire la probabilité que certains utilisateurs d'un site Web cliquent sur des publicités particulières, sous forme de pourcentage oui ou non.

La régression logistique peut également être utilisée dans les secteurs suivants :

• Secteur de la santé. La régression logistique peut être utilisée dans le domaine de la santé pour identifier les facteurs de risque de maladies et planifier des mesures préventives.
• Recherche pharmaceutique. Elle peut être utilisée dans la recherche pharmaceutique pour analyser l'efficacité des médicaments sur la santé en fonction de l'âge, du sexe et de l'origine ethnique.
• Prévisions météorologiques. La régression logistique est utilisée dans les applications de prévisions météorologiques pour prédire les chutes de neige et les conditions météorologiques.
• Sondages politiques. La régression logistique peut être utilisée dans les sondages politiques pour déterminer si les électeurs voteront pour un candidat particulier.
• Secteur des assurances. Il est utilisé dans le domaine des assurances pour prédire les chances qu'un assuré décède avant l'expiration de la police en fonction de critères spécifiques, tels que le sexe, l'âge et l'examen physique.
• Banque. La régression logistique peut être utilisée dans le secteur bancaire pour prédire les risques de défaut de paiement d'un emprunteur, en fonction de ses revenus annuels, de ses antécédents de défauts de paiement et de ses dettes passées.
• Télédétection. En télédétection, la régression logistique est utilisée pour analyser les images satellites, permettant ainsi de classer efficacement les types de couverture terrestre tels que les forêts, les terres agricoles, les zones urbaines et les plans d'eau.

Avantages et inconvénients de la régression logistique

La régression logistique offre les avantages suivants :

• Facile à mettre en place. Le principal avantage de la régression logistique est qu'il s'agit d'un modèle simple, beaucoup plus facile à mettre en place et à entraîner que d'autres modèles d'apprentissage automatique tels que les réseaux neuronaux et les applications d'IA.
• Algorithmes efficaces. Un autre avantage réside dans le fait qu'il s'agit de l'un des algorithmes les plus efficaces lorsque les différents résultats ou distinctions représentés par les données sont linéairement séparables. Cela signifie que vous pouvez tracer une ligne droite séparant les résultats d'un calcul de régression logistique.
• Révèle les interrelations entre les variables. L'un des principaux attraits de la régression logistique pour les statisticiens est qu'elle permet de révéler les interrelations entre différentes variables et leur effet sur les résultats. Cela permet de déterminer rapidement si deux variables sont corrélées positivement ou négativement, comme dans le cas cité plus haut où le fait d'étudier davantage tend à être corrélé à de meilleurs résultats aux examens. Mais il est important de noter que d'autres techniques, telles que l'IA causale, sont nécessaires pour passer de la corrélation à la causalité.
• Transforme des calculs complexes en problèmes mathématiques simples. La régression logistique transforme des calculs complexes liés à la probabilité en un problème arithmétique simple. Le calcul en lui-même est complexe, mais les méthodes et applications statistiques modernes automatisent une grande partie des calculs. Cela simplifie considérablement l'analyse de l'effet de plusieurs variables et minimise l'effet des facteurs de confusion. Ainsi, les statisticiens peuvent rapidement modéliser et explorer la contribution de divers facteurs à un résultat donné. Par exemple, un chercheur médical peut vouloir connaître l'effet d'un nouveau médicament sur les résultats thérapeutiques dans différents groupes d'âge. Cela implique de nombreuses multiplications et divisions imbriquées pour comparer les résultats des personnes jeunes et âgées qui n'ont jamais reçu de traitement, des personnes jeunes qui ont reçu le traitement, des personnes âgées qui ont reçu le traitement, puis le taux de guérison spontanée de l'ensemble du groupe. La régression logistique convertit la probabilité relative de tout sous-groupe en un nombre logarithmique, appelé coefficient de régression, qui peut être ajouté ou soustrait pour obtenir le résultat souhaité. Ces coefficients de régression plus simples peuvent également simplifier d'autres algorithmes de science des données et d'apprentissage automatique.
• Référence pour la gestion des performances. La régression logistique est souvent utilisée comme référence pour mesurer les performances en raison de sa configuration rapide et facile.

La régression logistique présente également divers inconvénients :

• Hypothèse de linéarité. Étant donné que la régression logistique suppose une relation linéaire entre une variable dépendante et les variables indépendantes, son applicabilité dans certains scénarios peut être limitée.
• Surajustement et sensibilité aux valeurs aberrantes. La régression logistique est sensible aux valeurs aberrantes. Si le nombre d'observations est inférieur au nombre de caractéristiques, la régression logistique ne doit pas être utilisée, car cela pourrait entraîner un surajustement. Les techniques de régularisation L1 et L2 peuvent être appliquées pour aider à réduire le surajustement.
• Limité aux résultats binaires. La régression logistique est limitée à la modélisation de la classification et des résultats binaires et peut ne pas convenir aux scénarios avec des résultats non binaires sans modifications telles que la régression logistique ordinale.
• Ne peut prédire que des fonctions discrètes. La régression logistique est exclusivement conçue pour prédire des fonctions discrètes, ce qui limite son utilisation aux variables dépendantes appartenant à un ensemble de nombres discrets. Cette limitation pose des difficultés pour la prédiction de données continues.

Outils et logiciels de régression logistique

Avant l'avènement des ordinateurs modernes, les calculs de régression logistique étaient une tâche laborieuse et chronophage. Aujourd'hui, les outils d'analyse statistique modernes tels que SPSS et SAS intègrent des fonctionnalités de régression logistique comme une fonctionnalité essentielle.

Les langages de programmation et les frameworks de science des données basés sur R et Python offrent de nombreuses façons d'effectuer une régression logistique et d'intégrer les résultats dans d'autres algorithmes. Par exemple, Python propose diverses bibliothèques telles que Statsmodels, scikit-learn et TensorFlow pour exécuter une régression logistique, tandis que R fournit des packages tels que glm, lrm et GLMNET pour l'analyse de régression logistique.

Parmi les autres outils et logiciels couramment utilisés pour effectuer une régression logistique, on peut citer les suivants :

• Microsoft Excel. Logiciel tableur très répandu permettant d'effectuer des analyses statistiques et des modélisations de base.
• Solveur. Il s'agit d'un outil complémentaire dans Excel permettant de résoudre des problèmes d'optimisation, notamment de déterminer les paramètres les mieux adaptés à un modèle logistique. Il existe différentes méthodes permettant d'utiliser Solveur pour automatiser la régression logistique.
• IBM SPSS. Outil de science des données de type glisser-déposer, IBM SPSS permet aux utilisateurs de créer et d'entraîner des modèles d'apprentissage automatique et d'intelligence artificielle, y compris la régression logistique. Il offre un environnement cloud hybride polyvalent pour la création de modèles et l'analyse de données.
• Logiciel NCSS. Ce logiciel offre une gamme complète d'outils et de procédures d'analyse de régression, y compris la régression logistique.
• Logiciel Unistat Statistics. Le logiciel Unistat Statistics offre une application complète de l'analyse des caractéristiques de fonctionnement (ROC) dans le cadre du processus de régression logistique. Il permet de calculer l'aire sous la courbe et de tracer des courbes ROC avec des variables.
• Amazon SageMaker. Amazon SageMaker est un service ML entièrement géré qui propose des algorithmes intégrés pour la régression linéaire et la régression logistique. Il aide les scientifiques des données à préparer, créer et entraîner des données, ainsi qu'à déployer instantanément des modèles de régression logistique.

Les responsables doivent également envisager d'autres outils de préparation et de gestion des données dans le cadre des efforts importants de démocratisation de la science des données. Par exemple, les entrepôts de données et les lacs de données permettent d'organiser des ensembles de données plus volumineux à des fins d'analyse. Les outils de catalogage des données peuvent mettre en évidence tout problème de qualité ou d'utilisabilité associé à la régression logistique. Les plateformes de science des données peuvent aider les responsables de l'analyse à créer des garde-fous appropriés afin de simplifier l'utilisation à plus grande échelle de la régression logistique dans l'ensemble de l'entreprise.

Régression logistique vs régression linéaire

Lorsque l'on compare les modèles de régression logistique et de régression linéaire, il est important de comprendre leurs principales différences et leurs applications. Les principales différences entre la régression logistique et la régression linéaire sont les suivantes :

• La régression logistique fournit un résultat constant, tandis que la régression linéaire fournit un résultat continu.
• Dans la régression logistique, le résultat, ou variable dépendante, est dichotomique et ne peut prendre que deux valeurs possibles. Cependant, dans la régression linéaire, le résultat est continu, ce qui signifie qu'il peut prendre n'importe laquelle parmi un nombre infini de valeurs possibles.
• La régression logistique est utilisée lorsque la variable réponse est catégorielle, telle que oui ou non, vrai ou faux, réussite ou échec. La régression linéaire est utilisée lorsque, au lieu d'une variable catégorielle, la variable réponse est continue, telle que les heures, la taille et le poids. Par exemple, à partir des données relatives au temps passé par un étudiant à étudier et à ses résultats aux examens, la régression logistique et la régression linéaire peuvent prédire des résultats différents.
• Avec les prédictions de régression logistique, seules des valeurs ou catégories spécifiques sont autorisées. Par conséquent, la régression logistique prédit si l'étudiant a réussi ou échoué. Comme les prédictions de régression linéaire sont continues, telles que des nombres dans une plage, elles peuvent prédire la note de l'étudiant sur une échelle de 0 à 100.
• La régression logistique est couramment utilisée pour les tâches de classification, telles que prédire si un e-mail est un spam en étudiant ses variables prédictives et ses caractéristiques. La régression linéaire est généralement utilisée pour des tâches telles que prédire les ventes futures à partir de données historiques.

Les organisations qui cherchent à contrôler et à gérer les risques peuvent tirer profit de l'utilisation de modèles de prévision des risques précis. Examinez différents modèles de prévision des risques et les avantages que les entreprises peuvent tirer de leur utilisation.