Qu'est-ce qu'un perceptron ?
Un perceptron est un modèle simple de neurone biologique utilisé dans un réseau neuronal artificiel. Frank Rosenblatt a introduit ce concept en 1957, lorsqu'il a démontré comment il pouvait constituer un élément de base dans un réseau neuronal à couche unique. Le perceptron est considéré comme l'un des premiers algorithmes créés pour l'apprentissage supervisé des classificateurs binaires.
L'algorithme perceptron a été conçu pour classer les entrées visuelles, en les regroupant dans l'une des deux catégories. L'algorithme suppose que les données sont linéairement séparables, c'est-à-dire qu'elles peuvent être naturellement séparées en deux catégories distinctes. Ce concept peut être visualisé comme un plan bidimensionnel avec deux ensembles de points de données. Si ces ensembles de données peuvent être séparés par une ligne droite, ils sont dits linéairement séparables. Sinon, elles sont non linéairement séparables, comme le montre la figure 1.
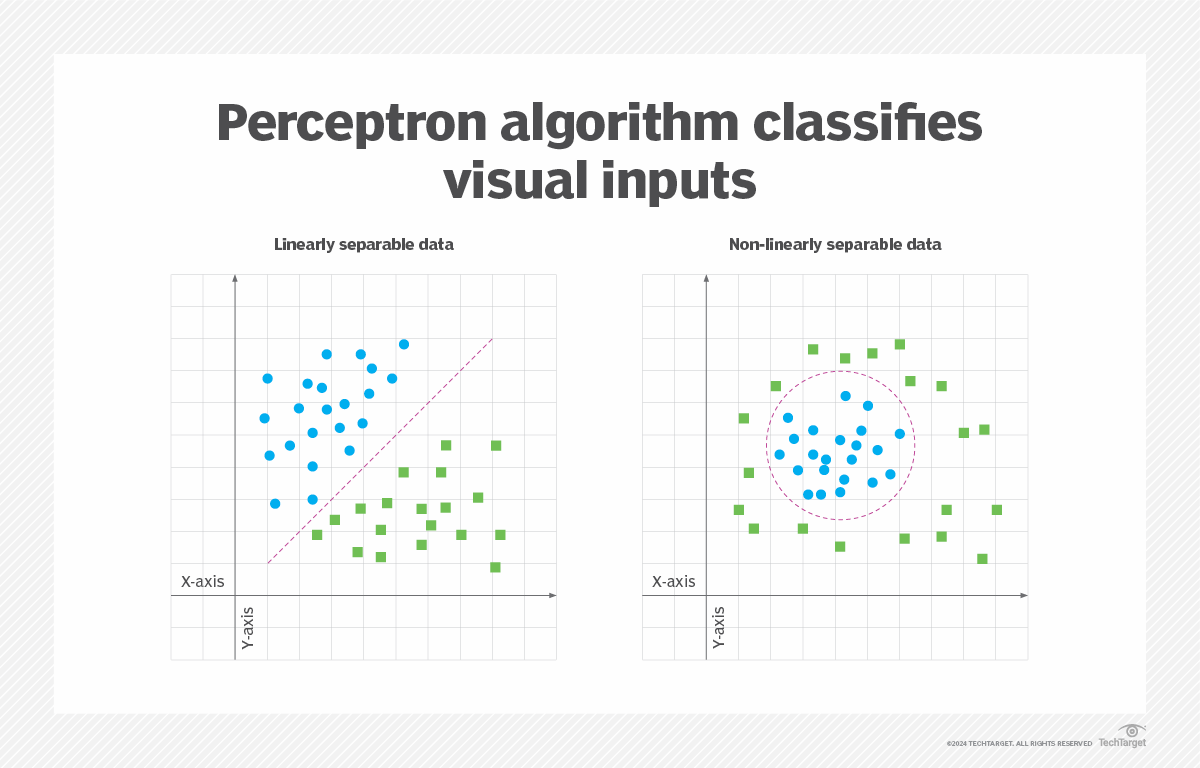
La classification est un élément important de l'apprentissage automatique et du traitement d'images. Les algorithmes d'apprentissage automatique utilisent différentes méthodes pour trouver et catégoriser les modèles de jeux de données. L'une de ces méthodes est l'algorithme perceptron. Il effectue une classification binaire en trouvant la séparation linéaire entre les points de données reçus via l'entrée du perceptron.
Comment fonctionne le perceptron ?
Le perceptron est un neurone artificiel qui tente de se rapprocher d'un neurone biologique. Le perceptron prend une ou plusieurs entrées pondérées et renvoie une seule sortie binaire, soit 1, soit 0. La figure 2 illustre l'algorithme du perceptron, dans lequel x est la valeur d'entrée, w est le poids de l'entrée et b est le biais (seuil) spécifié.
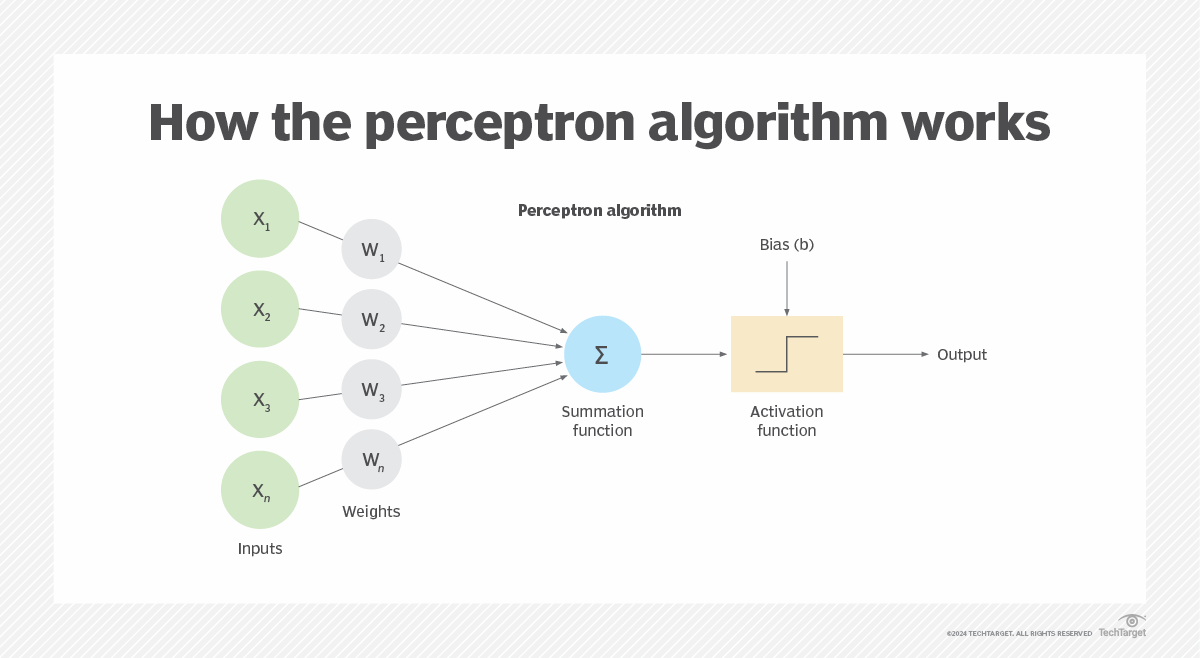
L'algorithme du perceptron peut être représenté de différentes manières, souvent à l'aide de conventions de nommage différentes, mais les concepts de base restent les mêmes. Le perceptron est composé des éléments suivants :
- Entrées. Le perceptron reçoit des données provenant d'une ou plusieurs entrées. Chaque entrée a une valeur numérique qui représente un attribut de données.
- Poids. Chaque valeur d'entrée se voit attribuer un poids numérique. Le poids détermine la force relative de l'entrée par rapport au perceptron dans son ensemble. La valeur d'entrée et le poids sont multipliés ensemble pour obtenir une valeur pondérée pour cette entrée.
- Fonction de sommation. La fonction additionne les valeurs pondérées de toutes les entrées. C'est pourquoi la fonction de sommation est parfois appelée fonction d'entrée nette.
- Biais (seuil). Une valeur numérique spécifique est attribuée au perceptron afin de contrôler la sortie indépendamment des entrées, ce qui permet une plus grande flexibilité.
- Fonction d'activation. La fonction effectue un calcul sur la somme et le biais d'entrée afin de déterminer s'il faut renvoyer un 1 ou un 0 binaire. L'approche exacte dépendra du type de fonction. Une fonction en escalier est couramment utilisée pour l'étape d'activation, bien qu'il existe plusieurs autres types de fonctions d'activation.
- Sortie. Le résultat binaire de la fonction d'activation.
Pour mieux comprendre comment ces composants fonctionnent ensemble, prenons l'exemple d'un décideur qui souhaite déterminer s'il doit acheter un produit en se basant sur quatre attributs. Chaque attribut représente une entrée binaire, sous la forme vrai ou faux (1 ou 0, respectivement). La figure 3 répertorie les attributs, leurs valeurs d'entrée et leurs pondérations.
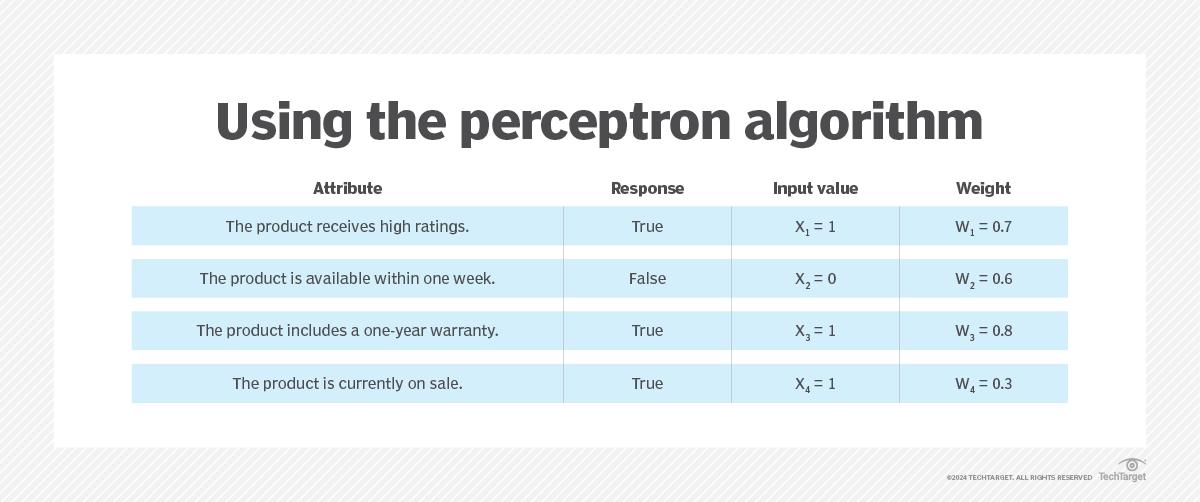
Dans ce scénario, l'attribut « garantie » (le troisième dans la figure 3) se voit attribuer le poids le plus important, tandis que l'attribut « vente » (le dernier) se voit attribuer le poids le plus faible. Il n'est donc pas surprenant que la manière dont les entrées sont pondérées puisse avoir un impact considérable sur le résultat. La fonction de sommation additionne les entrées pondérées à l'aide de la formule suivante :
z = x1w1 + x2w2 + x3w3 + x4w4
La fonction de sommation renvoie une valeur unique, qui est ensuite utilisée par la fonction d'activation. Pour déterminer la somme des entrées pour les attributs, leurs valeurs d'entrée et leurs pondérations peuvent être intégrées dans une formule :
z = x1w1 + x2w2 + x3w3 + x4w4
z = (1 x 0,7) + (0 x 0,6) + (1 x 0,8) + (1 x 0,3)
z = 0,7 + 0 + 0,8 + 0,3
z = 1,8
Ici, la fonction de sommation (z) renvoie une valeur de 1,8. Cette valeur peut être utilisée dans la fonction d'activation (a), avec le biais (b), qui dans ce cas a une valeur de 2. Les fonctions d'activation utilisent une logique différente pour calculer la valeur de sortie binaire. Cet exemple applique la logique suivante à la sommation et au biais :
a = 1 si z > b sinon 0
La formule stipule que la somme des entrées doit être supérieure au biais pour que la fonction renvoie un 1. Sinon, elle renverra un 0. Vous pouvez appliquer cette formule à l'exemple ci-dessus :
a = 1 si z > b sinon 0
a = 1 si 1,8 > 2 sinon 0
a est égal à zéro
La somme des entrées ne dépasse pas le seuil, donc le perceptron renvoie une valeur de 0. Cet exemple simple illustre les concepts de base du fonctionnement du perceptron et applique une logique simple.
Un perceptron peut également être entraîné à l'aide d'un algorithme d'apprentissage. Pendant la période d'entraînement, le perceptron suit un apprentissage supervisé qui utilise des données étiquetées dont les catégories sont déjà connues. Sur la base des résultats de ce processus, les poids et les biais du perceptron sont ensuite ajustés afin d'améliorer sa précision.
Une brève histoire du perceptron
L'idée du neurone artificiel est antérieure aux travaux de Rosenblatt. En 1943, le neurophysiologiste Warren McCulloch et le logicien Walter Pitts ont publié un article fondateur intitulé « A logical calculus of the ideas immanent in nervous activity » (Un calcul logique des idées immanentes dans l'activité nerveuse), qui fournit le premier modèle mathématique d'un réseau neuronal. Leur neurone artificiel, baptisé neurone McCulloch-Pitts (MCP), reçoit des entrées binaires et produit une sortie binaire.

Lors du développement du perceptron, Rosenblatt s'est appuyé sur les concepts du neurone MCP, mais il a amélioré le modèle afin d'accroître sa flexibilité. Il a travaillé sur le perceptron en 1957 au Cornell Aeronautical Laboratory, où il a reçu un financement de l'Office of Naval Research des États-Unis. Rosenblatt a d'abord exécuté l'algorithme sur un ordinateur IBM 704 qui pesait cinq tonnes et occupait toute une pièce. Ce projet a représenté la première étape vers la mise en œuvre d'une machine capable de reconnaître des images.
L'année suivante, Rosenblatt et ses collègues ont construit leur propre machine : le Mark I Perceptron. L'ordinateur contenait un ensemble de 400 cellules photoélectriques connectées à des perceptrons. Les poids des perceptrons étaient enregistrés dans des potentiomètres, ajustés par des moteurs électriques. Le Mark I Perceptron a été l'un des premiers réseaux neuronaux artificiels jamais créés. Il se trouve aujourd'hui au Musée national d'histoire américaine, qui fait partie du Smithsonian Institute.
Lorsque le perceptron a été introduit, beaucoup ont pensé qu'il représentait une avancée majeure dans le domaine de l'IA. Cependant, les limites techniques du perceptron sont rapidement apparues, car les perceptrons à couche unique ne peuvent regrouper les données que si celles-ci sont linéairement séparables. Plus tard, les scientifiques spécialisés dans les données ont découvert qu'en utilisant des perceptrons multicouches, ils pouvaient classer des données non linéairement séparables, ce qui leur permettait de résoudre des problèmes que les algorithmes à couche unique ne pouvaient pas traiter.
L'entraînement des réseaux neuronaux à imiter le cerveau humain permet aux modèles d'apprentissage profond d'appliquer l'apprentissage à des données qu'ils n'ont jamais vues auparavant. Découvrez comment les méthodes d'entraînement des réseaux neuronaux s'inspirent du cerveau humain. Explorez également les différences entre l'apprentissage supervisé, non supervisé, semi-supervisé et par renforcement.











